Mesoscopic Physics
Our group is mainly working on electrical properties of mesoscopic systems. 'Mesoscopic' means length scales of a system on the order of micro- or nanometers that on the one hand are big compared to atomic structures but on the other hand are of the same magnitude as internal length scales of the electronic system. One example would be the so called phase coherence length measuring about 1 µm in classical metals and approximately 50 µm in two-dimensional electron systems. It sets the scale over which electrons can interfere quantum mechanically. Currently, we focus on the following subjects:
- Carbon Nanotubes
- Electronic Interferometry
- Superconductor (S) - Ferromagnet (F) - Superconductor (S) Structures
- Superconductor (S) - Normal Conductor (N) - Superconductor (S) Structures
- Vortex motion
- Superinsulator
Carbon Nanotubes
Carbon nanotubes present a fascinating physical system, combining semiconductor physics, the properties of a defect-free macromolecule, and extreme mechanical stiffness. We are interested in three particular aspects: Nanotubes that are contacted with superconducting metals can carry a proximity-induced supercurrent and/or act as a weak link in a device structure. The interplay of the localized electronic structure of the nanotube and the physics of superconductivity is an active field of research. Here, niobium as contact material promises larger critical currents and more robust superconductivity with respect to temperature and magnetic field compared to previous processes. A complementary approach is given by using ferromagnetic contacts, and thereby probing the spin transport properties of electron systems trapped inside the macromolecules.
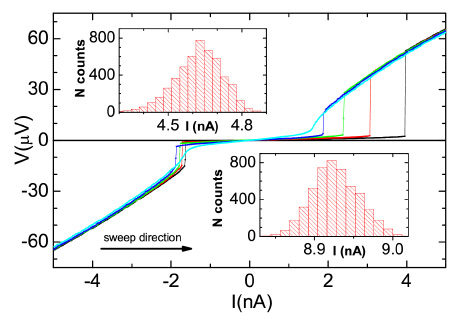Left: Scanning electron micrograph of a carbon nanotube with two superconducting Nb contacts attached. Right: Current-voltage characteristics of the Josephson junction with the nanotube as ‘weak link’.
Last but not least, nanotubes also excel in their mechanical properties. Here, both fully
quantized behaviour and classical resonator mechanics have been observed in different
vibration modes. Longitudinal vibrations, with a high spring constant and thereby excitation
energy, lead to quantized, phonon-like excitations, and can be observed in current through the
nanotube via the Franck-Condon effect. The bending or transversal mode (analogous to the motion
of a guitar or piano string) has been used as classical resonator, although its resonance
frequency is still very high compared to other types of nanomechanical devices. Current work
aims e.g. towards observing the transition from a classical to a quantum mechanical oscillator
in one and the same mechanical system – detecting true quantum-"mechanics".
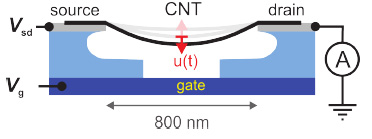Freely suspended nanotube between two metallic contacts. The gate electrode below changes both the
charge state of the tube and its mechanical tension.
Electronic Interferometry
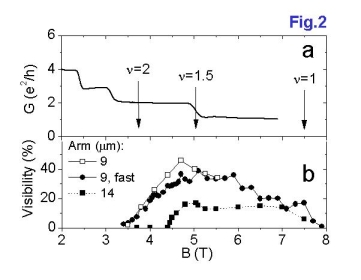
Edge states in the integer quantum Hall are closest electronic analog of light beams in quantum optics. It is thus tempting to use edge states to realize the interference of electrons in the solid with a very high visibility. The electronic Mach-Zehnder interferometer is such a device and a promising test ground for the study of decoherence and orbital entanglement. Such interferometers have a very high interference contrast at temperatures around 20 mK. We found that the interference is controlled by filling factor and is restricted to one interval over magnetic field, which approximately ranges from filling factor 2.0 to 1.0, with maximum near 1.5. The temperature dependence of visibility taken at fixed magnetic field shows an exponential decay above approximately 45 mK. As a function of dc-voltage, the decay of visibility is oscillatory with a gaussian envelope. The energy scales extracted from both types of measurement depend in a very similar way on magnetic field, indicating that the local structure of edge states plays a central role for the interference contrast.
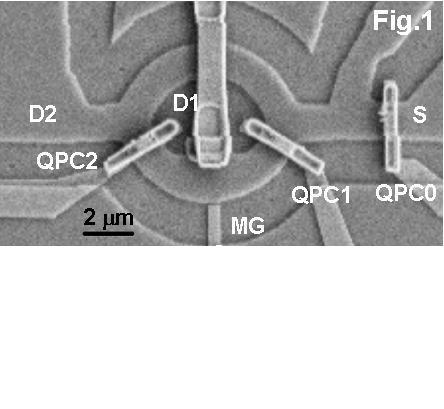
Left: Scanning electron micrograph of a Mach-Zehnder interferometer realized in a two-dimensional electron gas, which is embedded into a semiconductor heterostructure. Various quantum point contacts act a tunable beam splitter analog to those used in optics for light beams.
Right: Two-terminal conductance of the device without beam splitters, displaying the integer quantum Hall effect at high magnetic field. In within the Hall plateaus, the electric current flows in ν edge-channels, i.e., narrow, electrically separated strips along the sample edges, forming quasi-onedimensional beams of electrons. Left: Interference contrast (visibility) of different samples vs. magnetic field. The interference pattern has the highest visibility, if the outermost edge channel is screening by the compressible interior of the two-dimensional electron gas at ν=1.5.
Superconductor (S) - Ferromagnet (F) - Superconductor (S) Structures
Interesting physics is expected when antagonistic interaction mechanisms compete. For the case of superconductivity and ferromagnetism this becomes evident if one looks at the spin orientation of the electrons. In simple words, the dissipationless current that flows in superconductors is carried by Cooper-pairs, two electrons bound together by electron phonon interaction. For conventional superconductors the spin of the electrons is antiparallel so that the total spin of the Cooper-pair is zero. In ferromagnetism on the other hand it is well known that the exchange coupling between the electrons aligns the spins all parallel. Hence a natural question would be what happens if one combines those two ordering phenomena. Which one will dominate and potentially destroy or weaken the other one? It became evident that superconductivity can reach into a ferromagnet by the so called 'proximity effect'. This can be seen as a leaking of Cooper-pairs into the ferromagnet where they can 'survive' for a certain distance. If they are offered another superconductor after a thin ferromagnetic layer, supercurrent can flow across such a junction. Geometries of that type, meaning a normal metal between two superconductors, in general are called Josephson junctions and are an important element of applications of superconductivity. We use such ferromagnetic Josephson junctions in a ring setup (superconducting quantum interference device, SQUID) to investigate the process of supercurrent transfer in the presence of a competing ordering mechanism. The junctions are fabricated by state of the art nanostructuring techniques, like shadow mask evaporation. Their behaviour is measured in ultra low temperatures down to 300 mK in liquid Helium cryostates. A number of theoretical predictions could already be verified, like a spontaneous supercurrent for the so called pi-state that arises for certain thicknesses of the ferromagnetic interlayer. Other predictions, like the frequency doubling of the current-phase relation still await an unambiguous experimental prove.
Superconductor (S) - Normal Conductor (N) - Superconductor Structures
One interesting topic in our group is research on SNS contacts. When a normal conductor is in direct vicinity of a superconducting (sc) material, sc properties are being transferred to the normal part also what is known as the proximity effect. A theoretical description can be provided via Andreev reflection: Electrons coming from the normal part cannot enter the sc electrode due to the band gap around the Fermi energy. Instead it can be reflected from the interface as a hole with positive charge thereby creating a Cooper pair in the SC. In a sandwich structure of an N region between two sc electrodes, multiple Andreev reflection between the two interfaces can occur, resulting in Andreev bound states. A tunnel between two superconductors can sustain a supercurrent, which depends sinusoidally of the phase difference across the contact. In our SNS-junctions, deviations from this simple current-phase-relation (CPR) can be expected. The supercurrent flowing in a closed loop, which contains a silver metal bridge as junction, is detected magnetically, via the Hall effect in a micron-sized Hall-bar. Figure 1 shows the influence of microwave irradiation on the CPR of the depicted SNS ring structured of niobium and silver on a micro Hall bar. The radiation clearly induces higher harmonics in the current-phase relation, which can be interpreted in terms of a non-equilibrium population of the Andreev bound states.
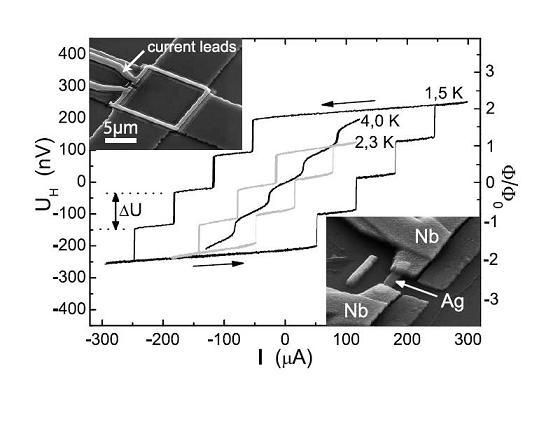
Left: Measured magnetic response of a superconducting niobium loop with a weak link formed by a
silver wire. The jumps at low temperature correspond to the penetration of single flux quanta into
the loop, once the critical current of the junction is exceeded. The scanning electron micrographs
show the Nb-loop on top of a semiconductor heterostructure, patterned in the shape of a Hall-cross.
The Hall-voltage UH in the two-dimensional electron gas embedded into the heterostructure served as
a sensor for the magnetic flux in the loop.Right: The measured supercurrent for different applied microwave powers and fixed temperature (top) and different temperatures and fixed power (bottom).
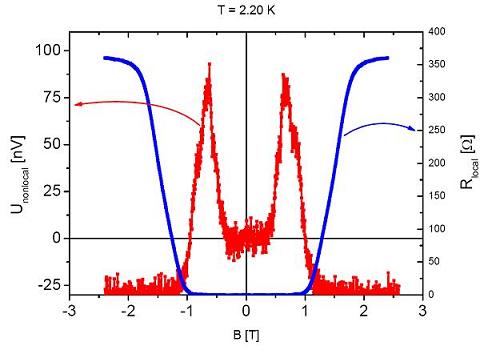
Dynamics of vortex motion in a-NbGe
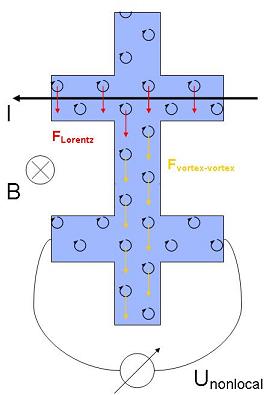
In the Shubnikov-phase of type-II superconductors, quantized lines of magnetic flux or vortices penetrate the material. If these vortices are subject to a transport current, they start to move under the influence of a Lorentz force perpendicular to external field and current, and thus they dissipate energy already at very small values of applied current, if pinning is absent. An example of very low pinning is amorphous NbGe. This enables us to observe vortex motion in the flux flow regime over large parts of the B-T phase plane. In the special geometry of the Transversal Flux Transformer Effect (see sample image below), a nonlocal voltage due to vortex motion can be measured in remote contacts, where actually no transport current flows. This phenomenon shows a rich dependence on temperature, magnetic field and applied current and ultimately might allow for the first experimental determination of the mass of a vortex in time-resolved measurements.
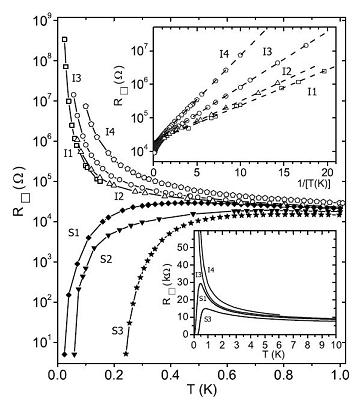
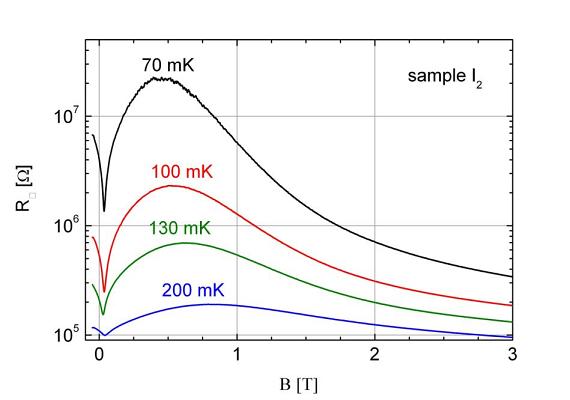
Superconductor - Insulator - Transition
We investigate the superconductor-insulator phase transition in thin TiN superconducting films, differing by the degree of disorder. Figure 1 shows the temperature dependence of the sheet resistance at the zero magnetic field. A separation between the superconducting and insulating phases is extremely sharp, indicating a direct superconductor-insulator transition without an intermediate metallic phase. Increasing level of disorder decreases superconducting critical temperature in superconducting films, while even higher disorder makes the film insulating. Figure 2 shows magnetoresistance isotherms of the insulated film. Magnetoresistance is huge and positive for low fields, while for higher fields is hugely negative. This feature can be explained by theory that relies on the competition of Coulomb charging and Josephson coupling in arrays of Josephson junctions formed in insulating film.
