Research topics
This page is in constant process of updating, there will be updates every now and then. Sorry for missing content or inconsistencies. If you have any questions, please contact us.Effect of strong spin-orbit interaction in Josephson junctions and 2D superconductors
Superconductivity in 2D electron gases (2DEGs) with large spin-orbit interaction (SOI) offers the opportunity to study a plethora of fascinating phenomena originating from space inversion- and time reversal-symmetry breaking.
Our playground is InGaAs/InAs/InGaAs quantum well with an epitaxial Al layer grown on top. Most of our samples are grown by the group of M. Manfra at Purdue University. The relatively high mobility of such systems allows us to work in the ballistic regime of the Josephson effect. Selective etching of the top Al layer makes it possible to obtain long meanders, single ballistic Josephson junctions, 1D or 2D arrays of junctions and coplanar waveguides. In what follows we present a selection of the Physics we can explore in these systems.
Superconducting diode effect in φ0 junctions
A fundamental theory prediction [Buzdin2008] about Josephson junctions between two 2D superconductors with Rashba SOI is the appearance of an anomalous shift φ0 in the current-phase relation (CPR) if an in-plane magnetic field is applied. If such so-called φ0 junctions contain several ballistic channels, then the superposition of the different anomalous shifts gives rise to an asymmetry between the positive and the negative branch of the current phase relation. The observable consequences of such asymmetry are: (i) the emerge of a so-called supercurrent diode effect (SDE), namely, an asymmetry between the critical currents for the two DC bias polarities; (ii) the magnetochiral anisotropy (MCA) of the inductance, where the Josephson inductance becomes an asymmetric function of the DC bias, with a non-zero slope near zero bias. It is worth stressing that junctions are homogeneous, and no flux is needed to observe nonreciprocity. The effect is produced by acting on the spin with a Zeeman field in the presence of Rashba SOI.
If the Zeeman field is sufficiently large, a satellite minimum originates in the full energy-phase relation given by the sum of all channel contributions. This minimum becomes eventually degenerate with the fundamental minimum at a certain threshold field. This field marks a so-called 0-π-like transition [Yokoyama2014] where the system switches between two anomalous phases. The jump in phase is less than π (motivating the suffix “-like”). Interestingly, at the new minimum, the curvature of the CPR changes sign. This means that the nonreciprocal signatures (inductance MCA and SDE) change sign.
References
[Buzdin2006] A. Buzdin, Phys. Rev. Lett. 101, 107005 (2008).
[Yokoyama2014] T. Yokoyama et al., Phys. Rev. B 89, 195407 (2014)
Selected works from our group
C. Baumgartner et al., Nature Nanotech. 17, 39 (2022)
C. Baumgartner et al., J. of Phys.: Cond.Matt., 34, 154005 (2022).
A. Costa et al., Nature Nanotech. 18, 1266 (2023).
Figure description: (Left) SEM picture of an array of Josephson junctions fabricated starting from Al/InAs heterostructures. (middle) Josephson inductance versus DC current for four angles between current and in-plane field. For (anti)parallel alignment L(I) is symmetric, whereas for perpendicular alignment L(I) is asymmetric (magnetochiral anisotropy). (Right) Superconducting diode effect in a single junction. From: C. Baumgartner et al., J. of Phys.: Cond.Matt., 34, 154005 (2022).
Abrikosov vortices in Rashba Superconductors
When measuring plain films (i.e., Al/InAs 2DEGs with no junctions), the combination of Rashba SOI and in-plane field is expected to reduce the symmetry of the superfluid. An interesting (and measurable) consequence of this symmetry breaking is the anisotropic squeezing of Abrikosov vortices, whose cores mirror the symmetry of the surrounding superfluid. A nice way to probe the curvature of the core is to apply a low frequency (MHz range) AC current bias and measure the inductive response of the 2DEG. For pinned vortices, the inductance is inversely proportional to the curvature of the core. What we found is that, the vortex cores are rendered elliptic, with the minor ellipse axis aligned to the in-plane field. By rotating the in-plane field with fixed current direction, we obtain a full tomography of the vortex core. Our results are the first experimental observation of a direct physical consequence of Lifshitz invariants
Reference
Our work
L. Fuchs et al., Phys. Rev. X, 12, 041020, (2023)
Figure description: (Left) Scheme of our experiment: pinned Abrikosov vortices are set in oscillation via an AC current and the corresponding voltage response is recorded. (Middle) The polar plot shows the inductance for different values of the out of plane field,as a function of the angle with the 0.5 T in-plane field. (Right) Vortex core for a 45° oriented in-plane field. The squeezing is a Lifshitz invariant effect.
Superconductivity in the presence of strong disorder
We study superconducting films with high level of disorder. At low temperature microscopic impurities lead to strong electron scattering and electron localization effects from quantum interference. Experimentally, the disorder leads to an increase in resistance, with respect to room temperature. One material platform that is currently in focus is strongly disordered niobium-nitride (NbN), where the disorder level is tuned by varying the amount of N2 during the deposition process as well as by oxidation effects at ambient conditions. We receive these films from IPHT Jena.
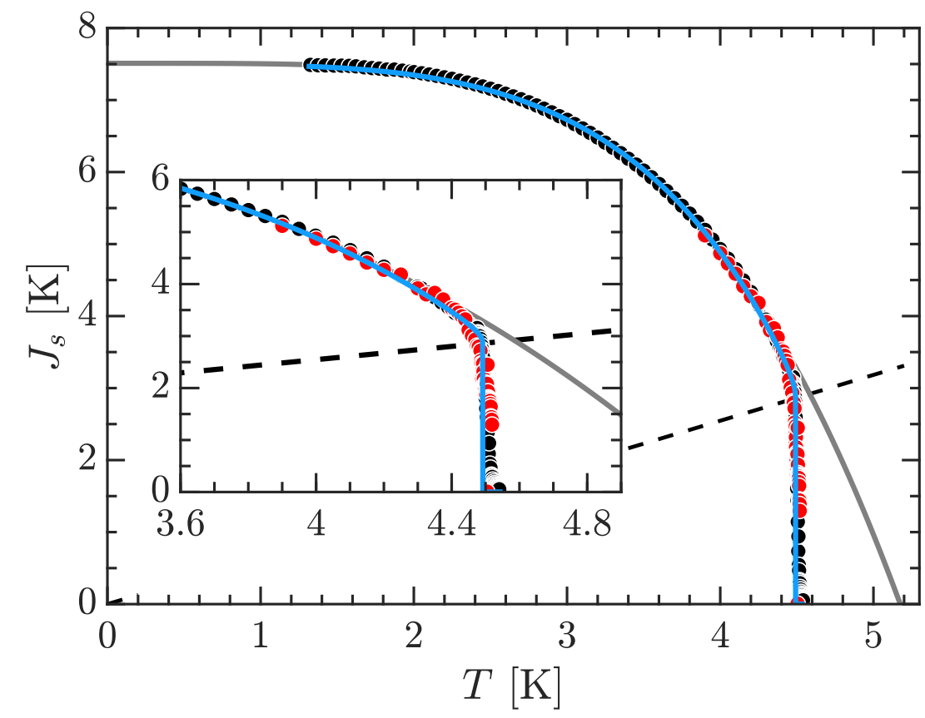
A famous theoretical prediction by Anderson [Anderson1959] states that non-magnetic impurities should not significantly change the superconducting properties of a material. However, in the case of very strong disorder, the validity of this theorem breaks down, and the physics is governed by the competition of localization (favoring to insulating behavior at T=0) and superconductivity, eventually leading to a superconductor-insulator transition (SIT) at high disorder. The SIT is a prime example of a quantum phase transition, which takes place at zero temperature and where the tuning knob is not temperature, but (in this case) disorder. The microscopic mechanism of SIT is in general not yet clear. We use a combination of DC and AC techniques to measure the superconducting properties of NbN at moderate to very strong disorder. As a first step towards understanding SIT in this material, we recently demonstrated that at moderate disorder the superconducting properties represent a perfect example of a topological phase transition, the celebrated Berezinskii-Kosterlitz-Thouless (BKT) transition [KosterlitzThouless1973]. Having understood BKT physics in a simple case sets the stage for further explorations towards even higher disorder, higher frequency or smaller sample sizes, which are all currently pursued in our group at the moment.
References
[Anderson1959] Anderson, P. W., J. Phys. Chem. Solids. 11 (1–2): 26–30, (1959)
[KosterlitzThouless1973] J. M. Kosterlitz, D. J. Thouless, J. of Phys. C: Solid State Physics. 6, 7, (1973)
Our work
A. Weitzel, L. Pfaffinger, et al., Phys. Rev. Lett. 131, 186002 (2023).
Figure description. Left: Typical meander structure of NbN (green) on Si/SiO2 substrate (blue), used for dc and ac measurements. Right: Typical sample holder with integrated LC circuit on PCB board, used for dc and ac measurements.
Figure description: Superfluid stiffness Js as function of T as function of temperature. Js is a quantity describing the resilience of the superconducting order parameter to phase fluctuations and can be related to the superfluid density, which manifests itself as an inductance. Black and red are inductance and dc transport measurements, respectively. Grey line is a fit towards the BCS prediction, blue line is a fit of BKT transition. The intersection of the dashed line and the data gives the point where Js should break down.